Answer:
a) L = 2.10x10⁴⁰ kg*m²/s
b) τ = 1.12x10²⁴ N.m
Step-by-step explanation:
a) The angular momentum (L) of the pulsar can be calculated using the following equation:
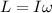
Where:
I: inertia momentum
ω: angular velocity
First we need to calculate ω and I. The angular velocity can be calculated as follows:
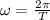
Where:
T: is the period = 33.5x10⁻³ s
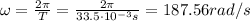
The inertia moment of the pulsar can be calculated using the following relation:
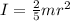
Where:
m: is the mass of the pulsar = 2.8x10³⁰ kg
r: is the radius = 10.0 km
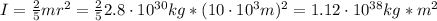
Now, the angular momentum of the pulsar is:
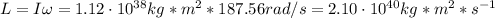
b) If the angular velocity decreases at a rate of 10⁻¹⁴ rad/s², the torque of the pulsar is:
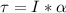
Where:
α: is the angular acceleration = 10⁻¹⁴ rad/s²
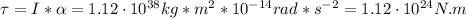
I hope it helps you!