Question

6) A pulsar is a rapidly rotating neutron star. The Crab nebula pulsar in the constellation Taurus has a period of 33.5 × 10−3 s, radius 10.0 km, and mass 2.8 × 1030 kg. The pulsar’s rotational period will increase over time due to the release of electromagnetic radiation, which doesn’t change its radius but reduces its rotational energy. (a) What is the angular momentum of the pulsar? (b) Suppose the angular velocity decreases at a rate of 10−14 rad/s2 . What is the torque on the pulsar?

Answer 1

a) L = 2.10x10⁴⁰ kg*m²/s

b) τ = 1.12x10²⁴ N.m

Step-by-step explanation:

a) The angular momentum (L) of the pulsar can be calculated using the following equation:

`L = I \omega`

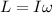
Where:

I: inertia momentum

ω: angular velocity

First we need to calculate ω and I. The angular velocity can be calculated as follows:

`\omega = (2 \pi)/(T)`

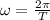
Where:

T: is the period = 33.5x10⁻³ s

`\omega = (2 \pi)/(T) = (2 \pi)/(33.5 \cdot 10^(-3) s) = 187.56 rad/s`

The inertia moment of the pulsar can be calculated using the following relation:

`I = (2)/(5)mr^(2)`

Where:

m: is the mass of the pulsar = 2.8x10³⁰ kg

r: is the radius = 10.0 km

`I = (2)/(5)mr^(2) = (2)/(5)2.8\cdot 10^(30) kg*(10\cdot 10^(3) m)^(2) = 1.12 \cdot 10^(38) kg*m^(2)`

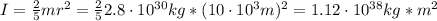
Now, the angular momentum of the pulsar is:

`L = I \omega = 1.12 \cdot 10^(38) kg*m^(2)*187.56 rad/s = 2.10 \cdot 10^(40) kg*m^(2)*s^(-1)`

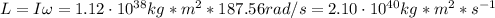
b) If the angular velocity decreases at a rate of 10⁻¹⁴ rad/s², the torque of the pulsar is:

`\tau = I*\alpha`

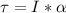
Where:

α: is the angular acceleration = 10⁻¹⁴ rad/s²

`\tau = I*\alpha = 1.12 \cdot 10^(38) kg*m^(2) * 10^(-14) rad*s^(-2) = 1.12 \cdot 10^(24) N.m`

I hope it helps you!