Answer:
Probability that the potential candidate will run for President election is 0.0096.
Explanation:
We are given that a potential candidate for President has stated that she will run for office if at least 30% of Americans voice support for her candidacy.
To make her decision she draws a random sample of 500 Americans. Suppose that in fact 35% of all Americans support her candidacy.
Let p = % of Americans voice support for her candidacy
The z score probability distribution for sample proportion is given by;
Z =
 ~ N(0,1)
~ N(0,1)
where,
 = sample proportion of Americans support her candidacy = 35%
= sample proportion of Americans support her candidacy = 35%
n = sample of Americans = 500
Now, probability that the potential candidate will obtain a p^ ≥ 0.30 and run for President is given by = P(
 ≥ 0.30)
≥ 0.30)
P(
 ≥ 0.30) = P(
≥ 0.30) = P(
 ≥
≥
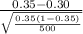 ) = P(Z ≥ 2.34) = 1 - P(Z
) = P(Z ≥ 2.34) = 1 - P(Z
 2.34)
2.34)
= 1 - 0.9904 = 0.0096
The above probability is calculated by looking at the value of x = 2.34 in the z table which has an area of 0.9904.
Hence, the required probability is 0.0096.