Question

Write the explicit formula for the geometric sequence.
a1 = −5, a2 = 15, a3 = −45

Answer 1

`a_(n)=-5(-3)^(n-1)`

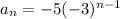
Explanation:

A geometric sequence or progession is defined as a sequence where each term can be found by multiplying a factor with the first term.

In this case, the first term is -5, the second term is 15 and the third term is -45.

`a_(1)=-5\\a_(2)=15\\a_(3)=-45`

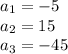
To find the factor, we divide the second term by the first, and the third term by the second.

`(15)/(-5)=-3`

`(-45)/(15)=-3`

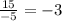
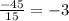
As you can notice, the factor is -3, so
`r=-3`.

Now, the explicit formula of this sequence can be found with

`a_(n)=a_(1)r^(n-1)`

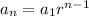
Where
`n` refers to the n-th term.

Replacing values, we have

`a_(n)=-5(-3)^(n-1)`

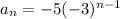
Therefore, the explicit formula of the geometric sequence is

`a_(n)=-5(-3)^(n-1)`

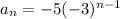
Which can be used to find any other term in the sequence.