Answer:
We conclude that the proportion of women who smoke cigarettes is smaller than or equal to the proportion of men at 0.01 significance level.
95% confidence interval for the difference in population proportions of women and men who smoke cigarettes is [0.0062 , 0.1298].
Explanation:
We are given that random samples of 125 women and 140 men reveal that 13 women and 5 men smoke cigarettes.
Let
 = population proportion of women who smoke cigarettes
= population proportion of women who smoke cigarettes
 = population proportion of men who smoke cigarettes
= population proportion of men who smoke cigarettes
So, Null Hypothesis,
 :
:
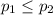 {means that the proportion of women who smoke cigarettes is smaller than or equal to the proportion of men}
{means that the proportion of women who smoke cigarettes is smaller than or equal to the proportion of men}
Alternate Hypothesis,
 :
:
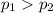 {means that the proportion of women who smoke cigarettes is higher than the proportion of men}
{means that the proportion of women who smoke cigarettes is higher than the proportion of men}
The test statistics that will be used here is Two-sample z proportion test statistics;
T.S. =
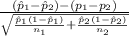 ~ N(0,1)
~ N(0,1)
where,
 = sample proportion of women who smoke cigarettes=
= sample proportion of women who smoke cigarettes=
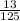 =0.104
=0.104
 = sample proportion of men who smoke cigarettes =
= sample proportion of men who smoke cigarettes =
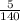 = 0.036
= 0.036
 = sample of women = 125
= sample of women = 125
 = sample of men = 140
= sample of men = 140
So, the test statistics =
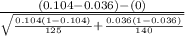
= 2.158
Now, at 0.01 significance level, the z table gives critical value of 2.3263 for right tailed test. Since our test statistics is less than the critical value of z as 2.158 < 2.3263, so we have insufficient evidence to reject our null hypothesis due to which we fail to reject our null hypothesis.
Therefore, we conclude that the proportion of women who smoke cigarettes is smaller than or equal to the proportion of men.
Now, coming to 95% confidence interval;
Firstly, the pivotal quantity for 95% confidence interval for the difference between population proportions is given by;
P.Q. =
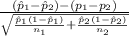 ~ N(0,1)
~ N(0,1)
where,
 = sample proportion of women who smoke cigarettes=
= sample proportion of women who smoke cigarettes=
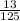 =0.104
=0.104
 = sample proportion of men who smoke cigarettes =
= sample proportion of men who smoke cigarettes =
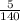 = 0.036
= 0.036
 = sample of women = 125
= sample of women = 125
 = sample of men = 140
= sample of men = 140
Here for constructing 95% confidence interval we have used Two-sample z proportion statistics.
So, 95% confidence interval for the difference between population proportions,
 is ;
is ;
P(-1.96 < N(0,1) < 1.96) = 0.95 {As the critical value of z at 2.5% level
of significance are -1.96 & 1.96}
P(-1.96 <
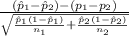 < 1.96) = 0.95
< 1.96) = 0.95
P(
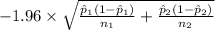 <
<
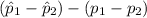 <
<
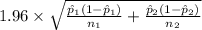 ) = 0.95
) = 0.95
P(
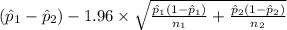 <
<
 <
<
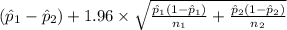 ) = 0.95
) = 0.95
95% confidence interval for
 =
=
[
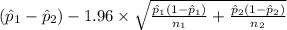 ,
,
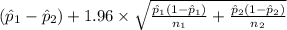 ]
]
= [
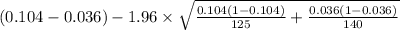 ,
,
 ]
]
= [0.0062 , 0.1298]
Therefore, 95% confidence interval for the difference in population proportions of women and men who smoke cigarettes is [0.0062 , 0.1298].