Answer:
0.5
Step-by-step explanation:
We are given the moles of two reactants, so this could be a limiting reactant problem.
We know that we will need moles, so, lets assemble all the data in one place.
2Ca₃(PO₄)₂ + 6SiO₂ + 10C → P₄ + 6CaSiO₃ + 10CO
n/mol: 1 3
Calculate the moles of P₄ that can be formed from each reactant :
1. From Ca₃(PO₄)₂
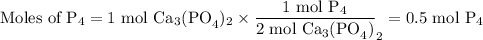
2. From SiO₂
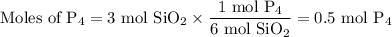
Each reactant forms 0.5 mol of P₄.