Question

An article predicts that "spit," spam that is delivered via internet phone lines and cell phones, will be a growing problem as more people turn to web-based phone services. In a poll of 5500 cell phone users, 19% indicated that they had received commercial messages and ads on their cell phones. Is there sufficient evidence that the proportion of cell phone users who have received commercial messages or ads in 2004 was greater than the proportion of 0.13 reported for the previous year? (Use α = 0.05. Round your test statistic to two decimal places and your P-value to four decimal places.)z =

P =There is evidence to suggest that the proportion cell phone users who have received commercial messages or ads in 2004 is greater than the proportion of 0.13 reported for the previous year.

Answer 1

We conclude that the proportion of cell phone users who have received commercial messages or ads in 2004 was greater than the proportion of 0.13 reported for the previous year.

Explanation:

We are given that in a poll of 5500 cell phone users, 19% indicated that they had received commercial messages and ads on their cell phones.

We have to test the claim that the proportion of cell phone users who have received commercial messages or ads in 2004 was greater than the proportion of 0.13 reported for the previous year.

Let p = proportion of cell phone users who have received commercial messages or ads in 2004.

So, Null Hypothesis,
`H_0` : p
`\leq` 0.13 {means that the proportion of cell phone users who have received commercial messages or ads in 2004 was smaller than or equal to the proportion of 0.13 reported for the previous year}

Alternate Hypothesis,
`H_A` : p > 0.13 {means that the proportion of cell phone users who have received commercial messages or ads in 2004 was greater than the proportion of 0.13 reported for the previous year}

The test statistics that would be used here One-sample z proportion statistics;

T.S. =
`\frac{\hat p-p}{\sqrt{(\hat p(1-\hat p))/(n)} }` ~ N(0,1)

where,
`\hat p` = sample proportion of cell phone users who have received commercial messages or ads in 2004 = 19%

n = sample of cell phone users = 5500

So, test statistics =
`\frac{0.19-0.13}{\sqrt{(0.19(1-01.9))/(5500)} }`

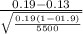
= 11.34

The value of z test statistics is 11.34.

Also, P-value of the test statistics is given by;

P-value = P(Z > 11.34) = 1 - P(Z
`\leq` 11.34)

= 1 - 0.9999 = 0.0001

Now, at 0.05 significance level the z table gives critical value of 1.645 for right-tailed test.

Since our test statistics is way more than the critical value of z as 11.34 > 1.645, so we have sufficient evidence to reject our null hypothesis as it will fall in the rejection region due to which we reject our null hypothesis.

Therefore, we conclude that the proportion of cell phone users who have received commercial messages or ads in 2004 was greater than the proportion of 0.13 reported for the previous year.