Question

You attach a 1.90 kg mass to a horizontal spring that is fixed at one end. You pull the mass until the spring is stretched by 0.400 m and release it from rest. Assume the mass slides on a horizontal surface with negligible friction. The mass reaches a speed of zero again 0.600 s after release (for the first time after release). What is the maximum speed of the mass (in m/s)

Answer 1

2.09 m/s

Step-by-step explanation:

As the spring is stretched initially , and the mass released from rest i.e v=0. Also, The next time the speed becomes zero again is when the spring is fully compressed, and the mass is on the opposite side of the spring with respect to its equilibrium position, after a time t=0.600 s. This illustrates half oscillation of the system.

Therefore, for the period of a full oscillation of the system

T= 2t => 2(0.6)=> 1.2 s

As the frequency is the reciprocal of the period, we have

f= 1/T => 1/1.2

f= 0.833 Hz

The angular frequency'ω' is given by,

ω= 2πf => 2π x 0.833=>5.23 rad/s

For the maximum velocity of the object in a spring-mass system:

V
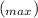`(_(max) )`= Aω

where A is the amplitude of the oscillation. As here, the amplitude of the motion corresponds to the initial displacement of the object (A=0.400 m)

V
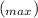`(_(max) )`= 0.4 x 5.23 =>2.09 m/s