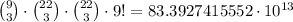Question

An English teacher needs to pick 9 books to put on his reading list for the next school year, and he needs to plan the order in which they should be read. He has narrowed down his choices to 19 novels, 22 plays, and 22 nonfiction books. If he wants to include an equal number of novels, plays, and nonfiction books, how many different reading schedules are possible? Express your answer in scientific notation rounding to the hundredths place.

Answer 1

The total number of reading schedules is
`83.3927415552\cdot 10^(13)`

Explanation:

Recall that if we have n elements, the number of ways in which we can choose k elements without minding the order is
`\binom{n}{k}=(n!)/((n-k)! k!)`.

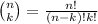At first, suppose that we have already chosen 9 books. If we want to number the order in which we are reading this books from 1 to 9, for position 1 we have 9 options, for position 2, we have 8 and so on. Using the multiplication principle, we have that the number of ways or arranging 9 books is 9!

Recall that we want the same amount from novels, plays and nonfiction. That is, we are choosing 3 books from each group. We can easy calculate the total number of ways of choosing the 9 books by simply multiplying the number of ways we choose 3 from each cathegory. Hence the total number of ways of choosing the 9 books is

`\binom{9}{3}\cdot \binom{22}{3}\cdot \binom{22}{3}`

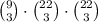
For each selection of 9 books, we have 9! different ways of organizing them, then the total number is

`\binom{9}{3}\cdot \binom{22}{3}\cdot \binom{22}{3}\cdot 9! = 83.3927415552\cdot 10^(13)`