Question

Betelgeuse is 100,000 times more luminous than our sun, which means that it releases an estimated 3.846 x 1031 W of luminous light. If an exoplanet existed with the same mass (5.972 x 10^24 kg) and twice the radius of earth (1.27 x 10^7 m) and half the distance (7.5 x 10^10 m) from Betelgeuse what would the intensity of the light at the surface of that "earth" look like? a) What is the intensity of Betelgeuse at the "earth’s" surface?

Answer 1

1.97*10^14 W/m^2

Step-by-step explanation:

To find the intensity of the light emitted by Betelgeuse you taken into account that the light from Betelgeuse expands spherically in space.

You use the following formula:

`I=(P)/(A)=(P)/(4\pi r^2)` (1)

I: intensity of light

r: distance from Betelgeuse to the exoplanet = (1/2)*7.5*10^10m

P: power = 100,000*3.486*10^31 W

By replacing the values of the parameters in (1) you obtain:
`I=(100000(3.486*10^(31)W)/(4\pi (0.5*7.5*10^(10)m)^2)=1.97*10^(14)(W)/(m^2)`

Answer 2

5.4 × 10⁸ W/m²

Step-by-step explanation:

Given that:

The Power (P) of Betelgeuse is estimated to release 3.846 × 10³¹ W

the mass of the exoplanet = 5.972 × 10²⁴ kg

radius of the earth = 1.27 × 10⁷ m

half the distance (i.e radius r ) = 7.5 × 10¹⁰ m

a) What is the intensity of Betelgeuse at the "earth’s" surface?

The Intensity of Betelgeuse can be determined by using the formula:

`Intensity \ I = (P)/(4 \pi r^2)`

`I = (3.846*10^(31))/(4 \pi (7.5*10^(10))^2)`

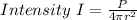
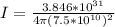
I = 544097698.8 W/m²

I = 5.4 × 10⁸ W/m²