Question

H(x) = -(x + 1)(x - 7)
What is the maximum height that the ball will reach?

Answer 1

16

Explanation:

All we have to do is write this in vertex form of a quadratic. It is now in factored form. To get it into vertex form we must complete various steps. Here you can skip it using desmos graphing calculator:

Answer 2

Answer: 16 units.

Explanation:

To find the vertex, first simplify the quadratic equation into its standard form:

`h(x)=-(x+1)(x-7)\\h(x)=(-x-1)(x-7)\\h(x)=-x^2+6x+7\\`

Using this formula, we can then find the axis of symmetry by using the formula S = -b/2a:

`S=(-6)/(-2)`

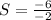
The axis of symmetry lies on x = 3.

You can then substitute x for 3 in the equation to find the vertex of the parabola:

`h(3)=-9+18+7\\h(3)=16`

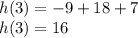
The ball will be 16 units high after travelling 3 units horizontally. This is the maximum height the ball will reach before falling.