Answer:
Step-by-step explanation:
the angular frequency ω of the pendulum is given by the formula
ω =
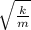 , k is spring constant , m is mass attached .
, k is spring constant , m is mass attached .
=
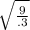
= 5.48 rad /s
time period = 2π / ω
= 2 x 3.14 / 5.48
= 1.146 s
b ) formula for speed
v = ω
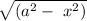 , a is amplitude , x is displacement from equilibrium point.
, a is amplitude , x is displacement from equilibrium point.
for maximum speed x = 0
max speed = ωa
= 5.48 x 3.8 x 10⁻² ( initial displacement becomes amplitude that is 3.8 cm )
= .208 m /s
20.8 cm / s
c )
when x = .02 m , velocity = ?
v = ω
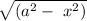
= 5.48
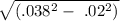
= 5.48 x .0323109
= .177 m /s
17.7 cm /s .