Answer:
C) (-1, -4) and (4, 6)
Explanation:
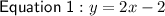

Substitute Equation 1 into Equation 2 and solve for x:
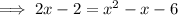
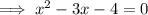
Find two numbers that multiply to -4 and sum to -3: -4 and 1
Rewrite the middle term as the sum of these two numbers:
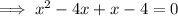
Factorize the first two terms and the last two terms separately:
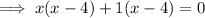
Factor out the common term
 :
:



Substitute the found values of x into Equation 1 and solve for y:
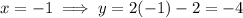
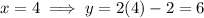
Therefore, the solution to the system of equations is:
(-1, -4) and (4, 6)