Answer:
Midpoint = (3.5, 4.5)
Perpendicular bisector = y =
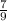 x +
x +
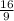
Explanation:
[] We can solve this using the midpoint formula:
-> See attached
[] Plug-in our coordinates and solve:

[] Now we will find the slope to solve for the perpendicular bisector.
-> We will use slope-intercept form, see attached
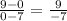
-> The slopes of two perpendicular lines are negative reciprocals of each other, so
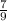 will be the slope of or perpendicular bisector
will be the slope of or perpendicular bisector
-> Now we can solve for the equation by using y – y1 = m ( x – x1), were y1 and x1 are the coordinates of our midpoint
y - 4.5 =
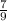 (x-3.5)
(x-3.5)
y - 4.5 =
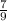 x-
x-
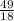
y =
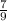 x-
x-
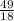 + 4.5
+ 4.5
y =
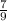 x +
x +
Have a nice day!
I hope this is what you are looking for, but if not - comment! I will edit and update my answer accordingly. (ノ^∇^)
- Heather