Answer:
C
Explanation:
The equation is in the standard form for a circle:
(x-h)^2+(y-k)^2=r^2
where (h,k) is the center, and r is the radius
If we compare the 2 equations:
(x-h)^2+(y-k)^2=r^2
(x + 10)2 + (y + 9)2 = 100
We can see that r^2 is equal to 100. Let's set them equal to each other.
r^2=100
Since r is being squared, take the square root of both sides. This will cancel out the exponent.
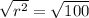
r=10
So, our radius is 10, or choice C