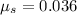Answer:
a)
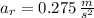 , b)
, b)
 , c)
, c)
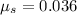
Step-by-step explanation:
a) The linear acceleration of the watermelon seed is:
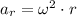
![a_(r) = \left[\left(33\,(rev)/(min) \right)\cdot \left(2\pi\,(rad)/(rev) \right)\cdot \left((1)/(60)\,(min)/(s) \right)\right]^(2)\cdot (0.023\,m)](https://img.qammunity.org/2021/formulas/physics/college/t1zzskga3acgl434fi4cdqgr8wcgiyqjk9.png)
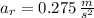
b) The watermelon seed is experimenting a centrifugal acceleration. The coefficient of static friction between the seed and the turntable is calculated by the Newton's Laws:
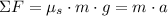
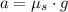
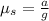
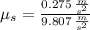

c) Angular acceleration experimented by the turntable is:
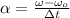
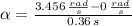

The tangential acceleration experimented by the watermelon seed is:

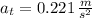
The linear acceleration experimented by the watermelon seed is:
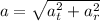
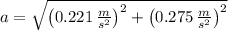
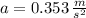
The minimum coefficient of static friction is: