Question

The mean annual precipitation for a large city in the Midwest is 30.85 inches with a standard deviation of 3.6 inches. Assume that the variable is normally distributed. a) What is the probability that a randomly selected month will have at least 30 inches of precipitation? b) What is the probability that of a random sample of 32 months taken will have a mean amount of precipitation between 30 and 31.5 inches?

Answer 1

Given Information:

Mean annual precipitation = 30.85 inches

Standard deviation of annual precipitation = 3.6 inches

Required Information:

a) P(X ≥ 30) = ?

b) P(30 < X < 31.5) = ?

Answer:

a) P(X ≥ 30) = 59.48%

b) P(30 < X < 31.5) = 16.62%

Step-by-step explanation:

What is Normal Distribution?

We are given a Normal Distribution, which is a continuous probability distribution and is symmetrical around the mean. The shape of this distribution is like a bell curve and most of the data is clustered around the mean. The area under this bell shaped curve represents the probability.

a) We want to find out the probability that a randomly selected month will have at least 30 inches of precipitation.

At least 30 inches of precipitation means equal to or greater than 30.

`P(X \geq 30) = 1 - P(X \leq 30)\\\\P(X \geq 30) = 1 - P(Z \leq (x - \mu)/(\sigma) )\\\\P(X \geq 30) = 1 - P(Z \leq (30 - 30.85)/(3.6) )\\\\P(X \geq 30) = 1 - P(Z \leq (-0.85)/(3.6) )\\\\P(X \geq 30) = 1 - P(Z \leq -0.24)\\`

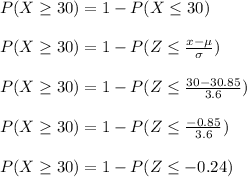
The z-score corresponding to -0.24 is 0.4052

`P(X \geq 30) = 1 - 0.4052\\\\P(X \geq 30) = 0.5948\\\\P(X \geq 30) = 59.48 \%\\`

Therefore, the probability that a randomly selected month will have at least 30 inches of precipitation is 59.48%

b) We want to find out the probability that of a random sample of 32 months taken will have a mean amount of precipitation between 30 and 31.5 inches.

`P(30 < X < 31.5) = P( (x - \mu)/(\sigma) < Z < (x - \mu)/(\sigma) )\\\\P(30 < X < 31.5) = P( (30- 30.85)/(3.6) < Z < (31.5 - 30.85)/(3.6) )\\\\P(30 < X < 31.5) = P( (-0.85)/(3.6) < Z < (0.65)/(3.6) )\\\\P(30 < X < 31.5) = P( -0.24 < Z < 0.18 )\\`

The z-score corresponding to -0.24 is 0.4052 and 0.18 is 0.5714

`P(30 < X < 31.5) = P( Z < 0.18 ) - P( Z < -0.24 ) \\\\P(30 < X < 31.5) = 0.5714 - 0.4052 \\\\P(30 < X < 31.5) = 0.1662\\\\P(30 < X < 31.5) = 16.62 \%`

Therefore, the probability that of a random sample of 32 months taken will have a mean amount of precipitation between 30 and 31.5 inches is 16.62%

How to use z-table?

Step 1:

In the z-table, find the two-digit number on the left side corresponding to your z-score. (e.g 0.2, 2.2, 0.5 etc.)

Step 2:

Then look up at the top of z-table to find the remaining decimal point in the range of 0.00 to 0.09. (e.g. if you are looking for 0.24 then go for 0.04 column)

Step 3:

Finally, find the corresponding probability from the z-table at the intersection of step 1 and step 2.