Answer:
C) x = 3, y = -6
Explanation:
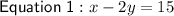
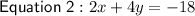
Rewrite Equation 1 to make x the subject:
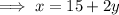
Substitute into Equation 2 and solve for y:
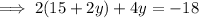
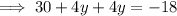
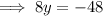
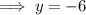
Substitute found value of y into Equation 1 and solve for x:
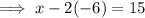
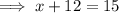
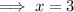
Therefore, the solution to the system of equations is:
x = 3, y = -6