Answer:
- The length of the hypotenuse is 14 ft

Explanation:
We'll solve this using the Pythagorean theorem, we know that,
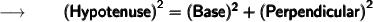
So, As it is given in the question that, the length of one leg of a right triangle is 9 ft and the length of the hypotenuse is 3 feet longer than the other leg and we are to find the length of the hypotenuse and the other leg.

Let us assume the other leg as x ft and therefore the hypotenuse will be (x + 3) ft.

Now, substituting the values in the formula :
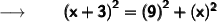
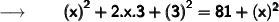
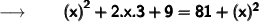
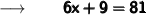
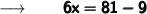

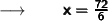

Therefore,
- The length of other leg is 12 ft . And the length of hypotenuse is (12 + 2) ft = 14 ft