Question

The length of one leg of a right triangle is 9 ft. The length of the hypotenuse is 3 feet longer than the other leg. Find the length of the hypotenuse and the other leg.

The length of the hypotenuse is ___ ft.

Answer 1

• The length of the hypotenuse is 14 ft

`\:`

Explanation:

We'll solve this using the Pythagorean theorem, we know that,

`\\ {\longrightarrow \pmb{\sf {\qquad (Hypotenuse {)}^(2)= (Base) {}^(2) + (Perpendicular {)}^(2) }}}`

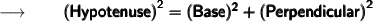
So, As it is given in the question that, the length of one leg of a right triangle is 9 ft and the length of the hypotenuse is 3 feet longer than the other leg and we are to find the length of the hypotenuse and the other leg.

`\:`

Let us assume the other leg as x ft and therefore the hypotenuse will be (x + 3) ft.

`\:`

Now, substituting the values in the formula :

`\\ {\longrightarrow \pmb{\sf {\qquad (x + 3 {)}^(2) = (9 {)}^(2) + (x) {}^(2) }}} \\ \\`

`{\longrightarrow \pmb{\sf {\qquad (x {)}^(2) + 2.x.3 + {(3)}^(2) =81 + (x) {}^(2) }}} \\ \\`

`{\longrightarrow \pmb{\sf {\qquad \cancel{ (x {)}^(2)} + 2.x.3 +9 =81 + \cancel{(x) {}^(2) }}}} \\ \\`

`{\longrightarrow \pmb{\sf {\qquad 6x + 9 =81 }}} \\ \\`

`{\longrightarrow \pmb{\sf {\qquad 6x =81 - 9 }}} \\ \\`

`{\longrightarrow \pmb{\sf {\qquad 6x =72 }}} \\ \\`

`{\longrightarrow \pmb{\sf {\qquad x = (72)/(6) }}} \\ \\`

`{\longrightarrow \pmb{\frak {\qquad x =12 }}} \\ \\`

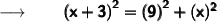
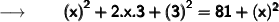
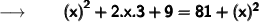
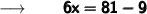
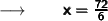
Therefore,

• The length of other leg is 12 ft . And the length of hypotenuse is (12 + 2) ft = 14 ft