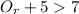Answer:
Explanation:
Let:
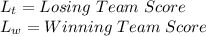
It is clear that, if the losing team is attempting to win its score must be greater than the score of the winning team. Mathematically, this can be written as:
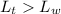
Now, let:
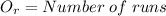
According to the problem:
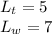
So:
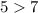
This is not true. However, we need to modify the inequality in order for it to make sense, in another words add to the losing team score a certain amount of runs:
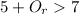
If we solve the inequality:
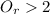
Which is true, because if the lose team wants to take the lead it need to score more than 2 runs.
Therefore, the inequality which represents the number of runs that the losing team must score in order to take the lead is: