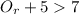Question

In the final inning of a baseball game, the score is 7 to 5. Which inequality represents the number of runs, that the losing

team must score in order to take the lead?
Or+5>7
Or+5<7
Or-5>7
Or-5<7

Answer 1

A) r + 5 > 7

Explanation:

if "r" is the number of runs they need to win, plus the amount they already have, it would need to be greater than 7.

so basically,

r + 5 = something greater than the other team's score, 7, so they can take the lead.

so it is r + 5 > 7

Answer 2

`O_r+5>7`

Explanation:

Let:

`L_t=Losing\hspace{3}Team\hspace{3}Score\\L_w=Winning\hspace{3}Team\hspace{3}Score`

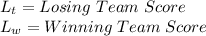
It is clear that, if the losing team is attempting to win its score must be greater than the score of the winning team. Mathematically, this can be written as:

`L_t>L_w`

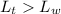
Now, let:

`O_r=Number\hspace{3}of\hspace{3}runs`

According to the problem:

`L_t=5\\L_w=7`

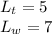
So:

`5>7`

This is not true. However, we need to modify the inequality in order for it to make sense, in another words add to the losing team score a certain amount of runs:

`5+O_r>7`

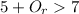
If we solve the inequality:

`O_r>2`

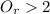
Which is true, because if the lose team wants to take the lead it need to score more than 2 runs.

Therefore, the inequality which represents the number of runs that the losing team must score in order to take the lead is:

`O_r+5>7`