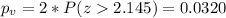Question

Pete is a politician. He claims that 32% of the households in his district have total household incomes below the poverty level. His opponent, Opal, wants to test this claim. Opal uses p to represent the proportion of households in the district with incomes below the poverty level. She formulates the null hypothesis, H0:p = 0.32, and an alternative, H1:p ≠ 0.32, to reflect her suspicion that Pete is wrong. Opal obtains a simple random sample of 225 households and finds that 87 of them have incomes below the poverty level. Her summary statistics are displayed. Sample size Sample count Sample proportion Standard error One-sample z-statistic n x p SE z 225 87 0.3867 0.0313 1.8077Use software to determine the p-value of the one-sample z-statistic.

Answer 1

`z=\frac{0.3867 -0.32}{\sqrt{(0.32(1-0.32))/(225)}}=2.145`

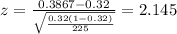
For a bilateral test the p value would be:

`p_v =2*P(z>2.145)=0.0320`

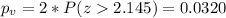
Explanation:

Information given

n=225 represent the sample selected

X=87 represent the households with incomes below the poverty level

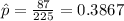`\hat p=(87)/(225)=0.3867` estimated proportion of households with incomes below the poverty level

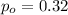`p_o=0.32` is the value that we want to test

z would represent the statistic

`p_v` represent the p value

System of hypothesis

We want to check if the true proportion is equal to 0.32 or not.:

Null hypothesis:
`p=0.32`

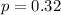
Alternative hypothesis:
`p \\eq 0.32`

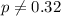
The statistic is given bY:

`z=\frac{\hat p -p_o}{\sqrt{(p_o (1-p_o))/(n)}}` (1)

Replacing we got:

`z=\frac{0.3867 -0.32}{\sqrt{(0.32(1-0.32))/(225)}}=2.145`

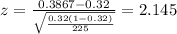
For a bilateral test the p value would be:

`p_v =2*P(z>2.145)=0.0320`