Question

The ratio of the lengths of the radii of two spheres is 5 : 8. What is the ratio of the surface area of the smaller sphere to the surface area of the larger sphere?

Answer 1

The ratio of the surface area of the smaller sphere to the surface area of the larger sphere is 25:64.

Explanation:

The surface area of square is given by formula as follows :

`A=4\pi r^2`

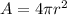
r is radius of sphere

The ratio of the lengths of the radii of two spheres is 5 : 8. The ratio of the surface area of the smaller sphere to the surface area of the larger sphere is :

`(A_1)/(A_2)=(r_1^2)/(r_2^2)`

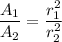
Here,
`(r_1)/(r_2)=(5)/(8)`

`(A_1)/(A_2)=(25)/(64)`

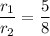
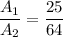
So, the ratio of the surface area of the smaller sphere to the surface area of the larger sphere is 25:64.