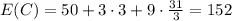Question

The failure of a circuit board interrupts work that utilizes a computing system until a new board is delivered. The delivery time, Y, is uniformly distributed on the interval 1 to 5 days. The cost incurred following a board failure is related to the delivery time for a new board by the formula C = 50 + 3Y + 9Y2. The E(C), the expected cost associated with the failure of a circuit board is.

Answer 1

The expected cost is 152

Explanation:

Recall that since Y is uniformly distributed over the interval [1,5] we have the following probability density function for Y

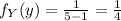`f_Y(y ) = (1)/(5-1) = (1)/(4)` if
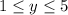`1\leq y \leq 5` and 0 othewise. (To check this is the pdf, check the definition of an uniform random variable)

Recall that, by definition

`E(Y^k) = \int_(-\infty)^(\infty) y^kf_Y(y)dy`

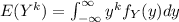
Also, we are given that
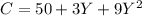`C = 50+3Y+9Y^2`. Recall the following properties of the expected value. If X,Y are random variables, then

`E(a+bX+cY) = a+bE(X)+cE(Y)`

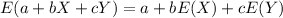
Then, using this property we have that
`E[C] = 50+3E[Y]+ 9E[Y^2]`.

Thus, we must calculate E[Y] and E[Y^2].

Using the definition, we get that

`E[Y] = \int_(1)^(5)(y)/(4) dy =(1)/(4)\left(y^2)/(2)\right|_(1)^(5) = (25)/(8)-(1)/(8) = 3`

`E[Y^2] = \int_(1)^(5)(y^2)/(4) dy =(1)/(4)\left(y^3)/(3)\right|_(1)^(5) = (125)/(12)-(1)/(12) = (31)/(3)`

Then

`E(C) = 50 + 3\cdot 3 + 9 \cdot (31)/(3) = 152`