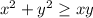2 Answers

Tlum · Answer 1 · 2021-08-14T16:23:32+0000

Answer:

Proof in explanation.

Explanation:

I'm going to assume you mean "greater than or equal to".

We know
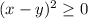$(x-y)^2 \ge 0$ .

We know this because any real number squared will result in a positive or zero result.

Let's expand the left hand side:

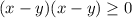
$(x-y)(x-y) \ge 0$

Distribute:

$x(x-y)-y(x-y) \ge 0$

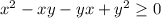
$x^2-xy-yx+y^2 \ge 0$

Combine like terms:

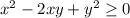
$x^2-2xy+y^2 \ge 0$

Commutative property of addition:

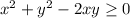
$x^2+y^2-2xy \ge 0$

Add
2xy on both sides:

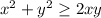
$x^2+y^2 \ge 2xy$

Now we wanted to show
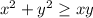$x^2+y^2 \ge xy$ . Our right hand side almost appeared that way except the factor of 2 present there.

Let's go back to our inequality that we got:

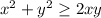
$x^2+y^2 \ge 2xy$

Divide both sides by 2:

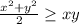
$(x^2+y^2)/(2) \ge xy$

Note: Half of a positive number is less than that positive number.

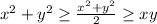
$x^2+y^2 \ge (x^2+y^2)/(2) \ge xy$

This inequality says we would like it to say in the end:

$x^2+y^2 \ge xy$

Please log in or register to add a comment.