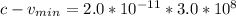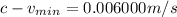Answer:
The closeness to the speed of light is
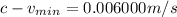
Step-by-step explanation:
From the question we are told that
The time taken to travel to Andromeda Galaxy is
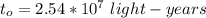
The life time of human is

Generally the life time of a human can evaluated mathematically as follows
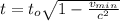
Where t is the life time of human
Making
 the subject of the formula
the subject of the formula
![v_(min) = [ \sqrt{1- ((t)/(t_o))^2 } ] c](https://img.qammunity.org/2021/formulas/physics/college/me8695c8bg4vw4m9bldmren25hu7r8i5tg.png)
substituting values
![v_(min) = [ \sqrt {1- {((75.0)/(2.54*10^(7) ))^2 } ]} c](https://img.qammunity.org/2021/formulas/physics/college/280fes4axpfbrku7yivj7z475accof2vbf.png)
![v_(min) = [ \sqrt{ 1 - 8.7202 *10^(-12)} ] c](https://img.qammunity.org/2021/formulas/physics/college/gaorva5zdwgp10j4q68345uekrks9gh067.png)
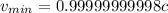
The closeness of
 to the speed of light is mathematically evaluated as
to the speed of light is mathematically evaluated as
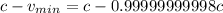
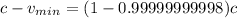
substituting
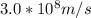 for c
for c