Correct question:
Thompson and Thompson is a steel bolts manufacturing company. Their current steel bolts have a mean diameter of 131 millimeters, and a standard deviation of 7 millimeters. If a random sample of 31" steel bolts is selected, what is the probability that the sample mean would differ from the population mean by more than 1.9 millimeters? Round your answer to four decimal places.
Answer:
0.1310
Explanation:
Given:
Sample size, n = 31
mean, u = 131
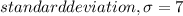
X - u = 1.9
If a random sample of 31 steel bolts is selected, the probability that the sample mean would differ from the population mean by more than 1.9 millimeter, would be determined by:
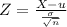

Z = 1.51
Probability =
P(|Z| > 1.51) =
P(Z < -1.51) + P(Z > 1.51)
= P(Z < -1.51) + 1 - P(Z > 1.51)
Using the standard normal table:
= NORMDIST(-1.51) = 0.0655;
NORMDIST(1.51) = 0.9345
Thus,
P = 0.0655 + 1 - 0.9345
= 0.1310