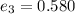Question

13–86 A radiation shield that has the same emissivity e3 on both sides is placed between two large parallel plates, which are maintained at uniform temperatures of T1 5 650 K and T2 5 400 K and have emissivities of e1 5 0.6 and e2 5 0.9, respectively. Determine the emissivity of the radiation shield if the radiation heat transfer between the plates is to be reduced to 15 percent of that without the radiation shield.

Answer 1

The emissivity of the radiation shield is
`e_3 = 0.580`

Step-by-step explanation:

From the question we are told that

The temperature of the first parallel plate is
`T_1 = 650K`

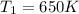
The temperature of the second parallel plate is
`T_2 = 400K`

The emissivity of first plate is
`e_1 = 0.6`

The emissivity of first plate is
`e_2 = 0.9`

Generally the total radiation heat that is been transferred without the shield is mathematically represented as

`Q_1 = (\sigma (T_1 ^4 - T_2 ^4))/((1)/(e1 ) + (1)/(e_2) -1 )`

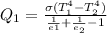
Where
`\sigma` is the Stefan-Boltzmann constant which has a value
`5.67 *10^(-8) \ W \cdot m^(-2) \cdot K^(-1)`

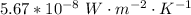
Substituting values

`Q_1 = ( 5.67 *10^(-8) (650 ^4 - 400 ^4))/((1)/(0.6 ) + (1)/(0.9) -1 )`

`Q_1 = 4876.8 \ W/m^2`

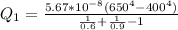
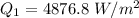
From the question we are told the that using the radiation shield would reduce the radiation heat transfer by 15%

So the new heat transfer is

`Q_2 = (15)/(100) * Q_1`

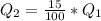
So
`Q_2 = (15)/(100) * 4876.8`

`Q_2 = 731.52 W/m^2`

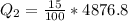
Now this new radiation heat transfer can be mathematically represented as

`Q_2 = (\sigma (T_1 ^4 - T_2 ^4))/( [(1)/(e_1 ) + (1)/(e_2 ) - 1 ] + n [(1)/(e_3) + (1)/(e_3) -1 ])`

Where
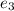`e_3` the emissivity of the radiation shield and n is the number of radiation shield

Substituting values

`731.52 = (5.67 *10^(-8) (650 ^4 - 400 ^4))/( [(1)/(0.6) + (1)/(0.9 ) - 1 ] + 1 [(1)/(e_3) + (1)/(e_3) -1 ])`

`731.52 = (1.4175*10^(-5))/( [(1)/(0.6) + (1)/(0.9 ) - 1 ] + 1 [(1)/(e_3) + (1)/(e_3) -1 ])`

`[(1)/(0.6) + (1)/(0.9 ) - 1 ] + 1 [(1)/(e_3) + (1)/(e_3) -1 ] = (1.4175*10^(-5))/(731.52)`

`[(1)/(0.6) + (1)/(0.9 ) - 1 ] + 1 [(1)/(e_3) + (1)/(e_3) -1 ] = 1.9377*10^(-8)`

`1 [(1)/(e_3) + (1)/(e_3) -1 ] = 1.9377*10^(-8) - [(1)/(0.6) + (1)/(0.9 ) - 1 ]`

`(1)/(e_3) + (1)/(e_3) = 1 .7222222416`

`e_3 = 0.580`