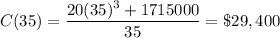Answer:
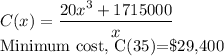
The dimensions that will lead to minimum cost of the box are a base length of 35 cm and a height of 140 cm.
Explanation:
Volume of the Square-Based box=171,500 cubic cm
Let the length of a side of the base=x cm
Volume

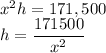
The material for the top and bottom of the box costs $10.00 per square centimeter.
Surface Area of the Top and Bottom
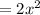
Therefore, Cost of the Top and Bottom
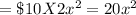
The material for the sides costs $2.50 per square centimeter.
Surface Area of the Sides=4xh
Cost of the sides=$2.50 X 4xh =10xh
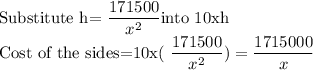
Therefore, total Cost of the box
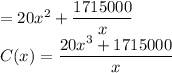
To find the minimum total cost, we solve for the critical points of C(x). This is obtained by equating its derivative to zero and solving for x.
![C'(x)=(40x^3-1715000)/(x^2)\\(40x^3-1715000)/(x^2)=0\\40x^3-1715000=0\\40x^3=1715000\\x^3=1715000/ 40\\x^3=42875\\x=\sqrt[3]{42875}=35](https://img.qammunity.org/2021/formulas/mathematics/college/ngiupvqur26crdkedkcrecucy9jyaql36a.png)
Recall that:
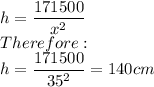
The dimensions that will lead to minimum costs are base length of 35cm and height of 140cm.
Therefore, the minimum total cost, at x=35cm