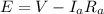Question

250 hp, 230 V, and speed of 435 r/min DC shunt motor has a nominal full load current 862 A. a. Calculate the total losses and efficiency at full load. b. Calculate the shunt field exciting current if the shunt field causes 20 percent of the total losses. c. Calculate the value of the armature resistance as well as the counter-emf (Ea), knowing that 50 percent of the total losses at full load are due to armature resistance.

Answer 1

(a) Losses 11760 watt, Efficiency = 94.06 %

(b) Shunt current 10.21 A

(c) Armature resistance = 0.0084 ohm

Armature voltage = 222.97 volt

Step-by-step explanation:

Output of the dc motor 2500 hp

As 1 hp = 746 watt

So output power

`P=250* 746=186500W`

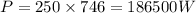
Full load current = 862 A

(A) Input of the motor is equal to

`=VI=230* 862=198260W`

Therefore losses = input - output

= 192860-186500 = 11760 watt

Efficiency =
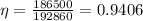`\eta =(186500)/(192860)=0.9406` = 94.06 %

(b) Power of shunt field is equal to

`P_(shunt)=11760* (20)/(100)=2352watt`

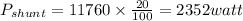
So shunt current
`I_(sh)=(2352)/(230)=10.21A`

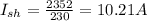
(C) It is given that 50% of the loss is due to armature current it means 50% loss will be due to shunt current

So loss due to shunt current
`=11760* 0.5=5880W`

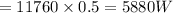
Shunt current is equal to
`I_(sh)=(5880)/(230)=25.56A`

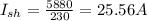
Armature current
`I_a=862-25.56=836.43A`

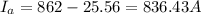
Power loss due to armature = 11760-5880 = 5880 W

Therefore
`I_a^2R_a=5880`

`836.43^2* R_a=5880`

`R_a=0.0084 ohm`

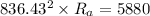
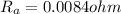
Emf is equal to
`E=V-I_aR_a`

`E=230-836.43* 0.0084=222.97V`