Answer:
8.4m/s
Explanation:
the information we are given is:
initial time:
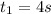
final time:
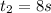
thus, the interval of time is:
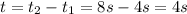
according to the statement, the distance at a certain time is given by:
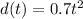
To find the average distance we need to find first the total distance traveled in those 4 seconds .
At a time of 4 seconds ⇒
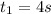
the distance at that time is:
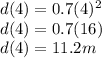
also, the distance at a time of 8 seconds ⇒
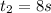
and the distance at this time is:
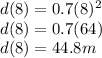
Now we can find the distance traveled between 4 and 8 seconds:
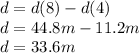
and finally we use the formula for the average speed:
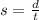
where
 is the distance traveled in
is the distance traveled in
 time:
time:
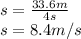
the average speed in meters per second: 8.4m/s