Question

A tobacco company claims that its best-selling cigarettes contain at most 40 mg of nicotine. The average nicotine content from a simple random sample 15 cigarettes is 42.6 mg with a standard deviation (s) of 3.7 mg. Is this evidence the nicotine content of the cigarettes exceeds 40 mg? Assume cigarette nicotine content is distributed normally. Use a 1% level of significance (α=0.01) to carry out the appropriate test of significance.

Answer 1

`t=(42.6-40)/((3.7)/(√(15)))=2.722`

`df=n-1=15-1=14`

`p_v =P(t_((14))>2.722)=0.0083`

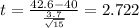
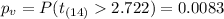
We see that the p value is lower than the significance level given of 0.01 so then we can conclude that the true mean for the nicotine content is significantly higher than 40 mg

Explanation:

Information provided

`\bar X=42.6` represent the average nicotine content

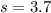`s=3.7` represent the sample standard deviation

`n=15` sample size

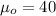`\mu_o =40` represent the value to check

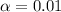`\alpha=0.01` represent the significance level for the hypothesis test.

t would represent the statistic

`p_v` represent the p value for the test

System of hypothesis

We want to verify if the nicotine content of the cigarettes exceeds 40 mg , the system of hypothesis are:

Null hypothesis:
`\mu \leq 40`

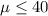
Alternative hypothesis:
`\mu > 40`

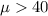
The statistic for this case would be:

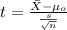`t=(\bar X-\mu_o)/((s)/(√(n)))` (1)

And replcing we got:

`t=(42.6-40)/((3.7)/(√(15)))=2.722`

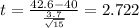
The degrees of freedom are:

`df=n-1=15-1=14`

The p value would be:

`p_v =P(t_((14))>2.722)=0.0083`

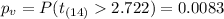
We see that the p value is lower than the significance level given of 0.01 so then we can conclude that the true mean for the nicotine content is significantly higher than 40 mg