Complete Question:
Some aircraft component is fabricated from an aluminum alloy that has a plane strain fracture toughness of 35MPa√m. It has been determined that fracture results at a stress of 250 MPa (36,250 psi) when the maximum (or critical) internal crack length is 2.0 mm (0.08 in.). For this same component and alloy, will fracture occur at a stress level of 325 MPa (47,125 psi) when the maximum internal crack length is 1.0 mm (0.04 in.)? Why or why not?
Answer:
Fracture will not occur
Reason: Because the fracture toughness = 32.20MPa√m which is less than the material toughness = 35MPa√m. The fracture toughness is not enough to make the material fracture.
Step-by-step explanation:
Critical Stress,

Internal crack length, a = 2 mm
a = l/2 = 2/2 = 1mm
a = 10⁻³ m
Toughness of the material,
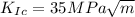
For the aluminium alloy to fracture, the material toughness,

Where
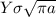 is the fracture toughness
is the fracture toughness
Where Y is a dimensionless parameter.
Using the critical stress crack propagation equation, let us find the dimensionless parameter:
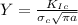
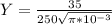
Y = 2.5
For a stress level of 325 MPa,
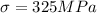 at maximum internal crack length, l = 1.0 mm =
at maximum internal crack length, l = 1.0 mm =
 m
m
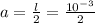
a = 0.0005 m
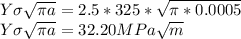
Since
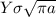 is less than the material toughness at a stress level of 325 MPa, fracture will not occur
is less than the material toughness at a stress level of 325 MPa, fracture will not occur