Answer:

The degrees of freedom are:
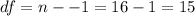
Now since we are conducting a right tailed test the p value can be calculated as follows:
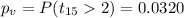
Since the p value is lower than the significance level of
 we have enough evidence to conclude that the true mean for the ages is significantly higher than 24
we have enough evidence to conclude that the true mean for the ages is significantly higher than 24
Explanation:
Information provided
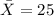 represent the mean for the ages
represent the mean for the ages
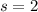 represent the sample standard deviation
represent the sample standard deviation
 sample size
sample size
 represent the value to check
represent the value to check
 represent the significance level
represent the significance level
t would represent the statistic
 represent the p value
represent the p value
Hypothesis to verify
We want to check if the average age of all the students at the university is significantly more than 24, the system of hypothesis would be:
Null hypothesis:
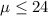
Alternative hypothesis:
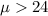
Since we don't know the population deviation the statistic would be given by:
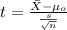 (1)
(1)
Replacing the data given we got:

The degrees of freedom are:
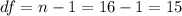
Now since we are conducting a right tailed test the p value can be calculated as follows:
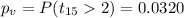
Since the p value is lower than the significance level of
 we have enough evidence to conclude that the true mean for the ages is significantly higher than 24
we have enough evidence to conclude that the true mean for the ages is significantly higher than 24