We have been given that the test scores on a final exam are normally distributed with a mean of 74 and a standard deviation of 3. We are asked to find the probability that a randomly selected test has a score higher than 77.
First of all, we will find z-score corresponding to sample score 77.
 , where,
, where,
z = z-score,
x = Random sample score,
 = Mean,
= Mean,
 = Standard deviation.
= Standard deviation.
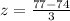
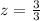

Now we need to find
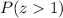 .
.
We will use formula
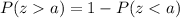 to find the probability greater than a z-score of 1.
to find the probability greater than a z-score of 1.
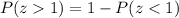
Using normal distribution table, we will get:

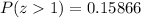
Therefore, the probability that a randomly selected test has a score higher than 77 would be 0.15866.