Answer:
![E[Y^2]=(2-q)/(q^2)](https://img.qammunity.org/2021/formulas/mathematics/college/vho1rw8iqu9fce3bnn1yi3fogl9tzhrx3f.png) where
where
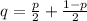 .
.
Explanation:
Since both Joanne and Jaden toss the coins at the same time, we will assume that this tosses are independent. Consider the event A that they get the same outcome. This means that they either get tails or heads. Since we consider each toss independent, the probability of each outcome is obtained by multiplying the probabilities. Then the probability of having both heads is p/2 and the probability of having both tails is (1-p)/2. Then
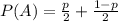
In this case, we can model the random variable Y as a geometric random variable with success probability
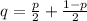 , since we want to count the number of trials until both get the same outcome. We will use the following
, since we want to count the number of trials until both get the same outcome. We will use the following
![E[Y^2] = Var(Y)+(E[Y])^2](https://img.qammunity.org/2021/formulas/mathematics/college/ueu5rxifootv81athz3rplrxhs5nydfm16.png)
In this case, we will take as a fact that
![Var(Y) = (1-q)/(q^2), E[Y] = (1)/(q)](https://img.qammunity.org/2021/formulas/mathematics/college/ofkrq573pol8sgkb19zwif6dme8qjv5yn0.png) .
.
Then,
![E[Y^2] = (1-q)/(q^2)+ (1)/(q^2) = (2-q)/(q^2)](https://img.qammunity.org/2021/formulas/mathematics/college/whj7tijfog24pd5xof4yiw5qor630094tz.png)
where
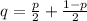 .
.