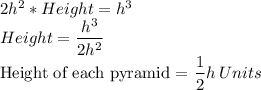Six pyramids are shown inside of a cube. The height of the cube is h units. Six identical square pyramids can fill the same volume as a cube with the same base. If the height of…

Question

asked Jun 18, 2021 216k views

2 Answers

Hackartist · Answer 1 · 2021-06-22T11:00:48+0000

Answer:

(A)The height of each pyramid is One-half h units.

Explanation:

Height of the Cube = h units

Volume of the Cube
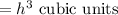
=h^3 $ cubic units

If Base of the cube =Base of the square pyramid

Base of the square pyramid = h units

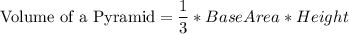
$\text{Volume of a Pyramid}=(1)/(3)*Base Area*Height$

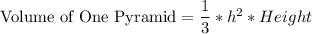
$\text{Volume of One Pyramid}=(1)/(3)*h^2*Height$

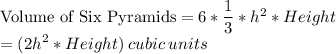
$\text{Volume of Six Pyramids}=6*(1)/(3)*h^2*Height\\=(2h^2*Height)\:cubic\:units$

Since Volume of the Cube = Volume of Six Square Pyramids

Then:

$2h^2*Height=h^3\\Height=(h^3)/(2h^2) \\$Height of each pyramid =(1)/(2)h \:Units$