Answer:
a) Mean: 900
Standard deviation: 24
b) Very unusual
c) Unusual
Explanation:
We have a population proportion p=0.36 and we are taking a sample of size n=2500. This can be modeled as binomial sampling.
For this sampling distribution, we have a mean and STD that can be calculated as:
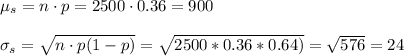
b) A value of 840 is a very unusual as is more than 2 standard deviations from the expected value of 900 (more exactly, at 2.5 standard deviations). Approximately 2% of the values are below 2 standars deviations from the mean.
Having 840 or less televisions tuned to "Eyewitness News" would have a probability of P=0.00621.
c) A value of 945 would be also unusual, but not as unusual as 840, as is between 1 and 2 standard deviation from the expected value.
Having 945 or more televisions tuned to "Eyewitness News" would have a probability of P=0.0304.