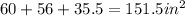Answer:
Total surface area is
Explanation:
This problem is on the mensuration of solid shapes, rectangular pyramid.
We can solve for the total surface area by solving the area of individual parts of the pyramid
1. The area of the rectangular base
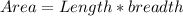
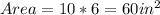
2. Area of 1st triangular side
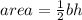
Areas =

Area =
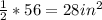
for the two sides the area is =
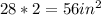
3. Area of 2nd triangular side
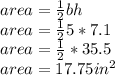
for the two sides the area is
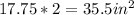
Therefore the total surface area is
Areas of rectangular base plus 1st and 2nd triangular sides
Total surface area =