Answer:

Explanation:
You can start by finding the area of the triangular base. You might know that the area for a triangle is
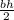 , where b is the area of the triangle's base and h is the height of the triangle. In this case, you know the height, but you don't know the base yet, only one of the side lengths of the triangle. However, using the Pythagorean theorem, you can find that the length of half of the base is
, where b is the area of the triangle's base and h is the height of the triangle. In this case, you know the height, but you don't know the base yet, only one of the side lengths of the triangle. However, using the Pythagorean theorem, you can find that the length of half of the base is
 . Multiplying this by the height of the triangle and dividing by 2, you get an area for half the base to be
. Multiplying this by the height of the triangle and dividing by 2, you get an area for half the base to be
 , and a full area of
, and a full area of
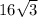 . Now you need to find the height of the overall pyramid. The length of the long, central diagonal to the top of the pyramid can also be found using the Pythagorean theorem:
. Now you need to find the height of the overall pyramid. The length of the long, central diagonal to the top of the pyramid can also be found using the Pythagorean theorem:
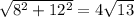 . You can use the Pythagorean theorem once again to find the overall height of the pyramid, using the width of 4cm.
. You can use the Pythagorean theorem once again to find the overall height of the pyramid, using the width of 4cm.
 . Finally, you can use the formula for the area of a triangular pyramid, and find that the volume is
. Finally, you can use the formula for the area of a triangular pyramid, and find that the volume is
 . Hope this helps!
. Hope this helps!