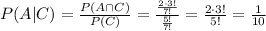Question

The letters {a, b, c, d, e, f, g} are put in a random order. Each permutation is equally likely. Define the following events:

A: The letter b falls in the middle (with three before it and three after it)
B: The letter c appears to the right of b, although c is not necessarily immediately to the right of b. For example, "agbdcef" would be an outcome in this event.
C: The letters "def" occur together in that order (e.g. "gdefbca")

Calculate the probability of each individual event. That is, calculate p(A), p(B), and p(C). (b) What is p(A|C)

Answer 1

`P(A)=(6!)/(7!) = (1)/(7)`

`P(C)=(5!)/(7!) = (1)/(6\cdot 7)`

`P(B) = (1)/(2)`

`P(A|C)=(1)/(10)`

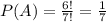
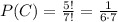
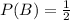
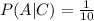
Explanation:

Recall that since the permutations are all equally likely, we can calculate the probability of each event as follows

`P(A) = \frac{\text{\# of events that conform the event A}}{\text{total number of events}}`.

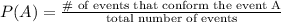Note that since we have 7 letters, the total number of permutations is 7!. That is because when we are arranging the letters, for the first letter(from left to right) we have 7 possibilities, for the second one we have 6 and so on. So by the multiplication principle, the total number of ways of arranging 7 letters is 7*6*5*4*3*2*1 = 7!.

a) Consider the event that b falls in the middle. In this case, imagine the following scenario _ _ _ b _ _ _. We have b fixed in the middle, but we can arrange the other letters freely. In this case, it is the same as we considered having the letters a,c,d,e,f,g only and organizing them in the free spaces. That is, we a total of 6! permutations that have the letter b in the middle.

Then
`P(A) = (6!)/(7!) = (1)/(7)`

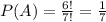
b) Consider the following numbering of the positions of the letters.

1 2 3 4 5 6 7 . Note that if we place the b in the position 7, we cannot place the letter c on the right of the letter b. Then, b must be in the first 6 positions. Suppose we have the following case

_ _ b _ _ _ _ . In this case we have 4 positions where to place the letter c. The rest of the letters we can arrange them in 5! in the remainding 5 positions. So, generalizing, consider we put the letter b in position k (where
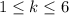`1\leq k \leq 6`. Then, we have (7-k) posibilities for the letter c to be placed and we have 5! possibilities for the remainding 5 letters. Then the total number of permutations that occur for event b is

`\sum_(k=1)^(6)5!(7-k) = 5!(42-(6(6+1))/(2)) = 21\cdot 5!`

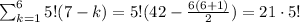
Then,

`P(C) = (21 \cdot 5!)/(7!) = (7\cdot 3 \cdot 5!)/(7!) = (3)/(6)=(1)/(2)`

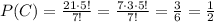
c) Since we must have the letters "def" all together, we can arrange first the other letters and then "squeeze" the letters in between. For example, consider the permutation abcg. Then, in this case we can think that there is a space in between the letters as follow _a_b_c_g_. So, note that for one permutation of the letters abcg we have 5 available space were we can put the letters "def" together. We have a total 4! of the letters abcg and for each permutation we have 5 options. Then, the total number of permutations that have the letters "def" all together in that order is 4!*5 = 5!. So

`P(C) = (5!)/(7!) = (1)/(6\dot  7) =`

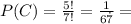
d) By definition,

`P(A|C) = (P(A\cap C))/(P(C))`

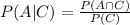
We must calculate
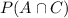`P(A\cap C)`. The intersection of A and C means that both events occur. In this case we have, again, this scenario _ _ _ b _ _ _. We want to calculate the number of permutations of the rest of the letters where "def" appear together in that order. REcall that in this scenario we can place "def" either to the right of the b or to the left. So, we have two options. Say we put "def" on the left. So, we have 3 free spaces where to place the rest of the letters, where we can arrange the 3 remaining letters in 3! ways. So, the total number of permutations that have the letters "def" together and the letter b in the middle is 2*3!. Then
`P(A\cap C) = (2\cdot 3!)/(7!)`

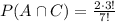
So
`P(A|C) = (P(A\cap C))/(P(C)) = ((2\cdot 3!)/(7!))/((5!)/(7!))= (2\cdot 3!)/(5!)= (1)/(10)`