Question

The man is walking with speed v1 = 1.35 m/s to the right when he trips over a small floor discontinuity. Estimate his angular velocity just after the impact. His mass is 72 kg with center-of-mass height h = 0.71 m, and his mass moment of inertia about the ankle joint O is 66 kg·m2, where all are properties of the portion of his body above O; i.e., both the mass and moment of inertia do not include the foot. The angular velocity is positive if counterclockwise, negative if clockwise.

Answer 1

The angular velocity,
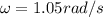`\omega = 1.05 rad/s` clockwise

Step-by-step explanation:

The mass of the man, m = 72 kg

The center of mass of the man will be at the middle of his body, particularly around his abdomen.

Height of the center of mass, h = 0.71 m

The speed of the man, v₁ = 1.35 m/s

Moment of inertia about the ankle joint, I = 66 kg/m²

Based on the principle of conservation of angular momentum (about the ankle joint):

Angular momentum before impact = Angular momentum after impact

Angular momentum before impact = -mv₁h

Angular momentum before impact = -(72 * 1.35 * 0.71)

Angular momentum before impact = -69.012 kg m²/s...............(1)

Angular momentum after impact =
`I \omega`

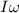
Angular momentum after impact =
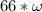`66 * \omega`.................(2)

`66 \omega = -69.012\\\omega = -69.012/66\\\omega = -1.05 rad/s`

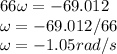
The angular velocity,
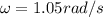`\omega = 1.05 rad/s` clockwise