Answer:
The 95% confidence interval for the difference between the Route B and Route A commuting times is -4.640279 < μ₁ - μ₂ <-1.359721
Explanation:
Here we have the formula for the confidence interval of the difference between two means given as follows;
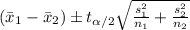
Where:
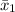 = Mean of Route A = 40
= Mean of Route A = 40
 = Mean of Route B = 43
= Mean of Route B = 43
s₁ = Standard deviation of time to work for Route A = 3 minutes
s₂ = Standard deviation of time to work for Route B = 2 minutes
n₁ = Number of days taken through Route A = 20 days
n₂ = Number of days taken through Route B = 20 days
At 95% confidence level, and df = 20 - 1 = 19 we have;
 = ±2.03452
= ±2.03452
Plugging in the values, we have;
 , which gives the 95% confidence interval for the difference between the Route B and Route A commuting times as follows;
, which gives the 95% confidence interval for the difference between the Route B and Route A commuting times as follows;
-4.640279 < μ₁ - μ₂ <-1.359721.