Answer:
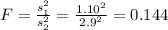
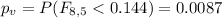
Since the p value is lower than the significance level we have enough evidence to reject the null hypothesis and we can conclude tha the variance in city 1 is less than the variance in city 2
Explanation:
Data given
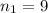 represent the sampe size for group 1
represent the sampe size for group 1
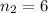 represent the sample size for group 2
represent the sample size for group 2
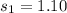 represent the sample deviation for group 1
represent the sample deviation for group 1
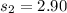 represent the sample deviation for group 2
represent the sample deviation for group 2
 represent the significance level provided
represent the significance level provided
Confidence =0.95 or 95%
Solution to the problem
System of hypothesis
We want to test if the variance in city 1 is less than the variance in city 2., so the system of hypothesis are:
H0:

H1:
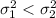
Calculate the statistic
The statistic is given by:

Replacing we got:
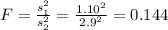
We need to find the degrees of freedom. For the numerator we have
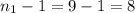 and for the denominator we have
and for the denominator we have
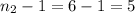 and the F statistic present 8 degrees of freedom for the numerator and 5 for the denominator.
and the F statistic present 8 degrees of freedom for the numerator and 5 for the denominator.
P value
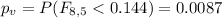
Since the p value is lower than the significance level we have enough evidence to reject the null hypothesis and we can conclude tha the variance in city 1 is less than the variance in city 2