Question

In a study investigating the effect of car speed on accident severity, 5,000 reports of fatal automobile accidents were examined, and the vehicle speed at impact was recorded for each one. For these 5,000 accidents, the average speed was 43 mph and the standard deviation was 15 mph. A histogram revealed that the vehicle speed at impact distribution was approximately normal.

a. Roughly what proportion of vehicle speeds were between 27 and 57 mph?
b. Roughly what proportion of vehicle speeds exceeded 57 mph?

Answer 1

a) P(27<x<57)=0.68

b) P(X>57)=0.18

Explanation:

We have a sample of n=5000 accidents, where the sample mean is 43 mph and the sample standard deviation is 15 mph, with a distribution shape approximately normal.

a) We have to calculate what proportion of vehicle speeds were between 27 and 57 mph.

If the distribution is approximately normal, we can calculate a z-score and then the probability.

`z_1=(X_1-\mu)/(\sigma)=(27-43)/(15)=(-16)/(15)=-1.0667 \\\\\\z_2=(X_2-\mu)/(\sigma)=(57-43)/(15)=(14)/(15)=0.9333`

`P(27<X<57)=P(-1.0667<z<0.9333)\\\\P(27<X<57)=P(z<0.9333)-P(z<-1.0667)\\\\P(27<X<57)=0.82467-0.14305=0.68162`

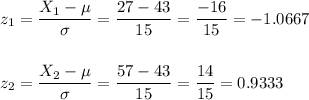
b) We have to calculate what proportion of vehicle speeds were 57 mph or more.

We use the same z=0.9333 for X=57, so we can calculate the probability as:

`P(x>57)=P(z>0.9333)=1-P(z<0.9333)=1-0.82467=0.17533`