Answer:
64.65% probability of at least one injury commuting to work in the next 20 years
Explanation:
In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:

In which
x is the number of sucesses
e = 2.71828 is the Euler number
 is the mean in the given interval.
is the mean in the given interval.
Each day:
Bikes to work with probability 0.4.
If he bikes to work, 0.1 injuries per year.
Walks to work with probability 0.6.
If he walks to work, 0.02 injuries per year.
20 years.
So

Either he suffers no injuries, or he suffer at least one injury. The sum of the probabilities of these events is decimal 1. So
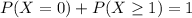
We want
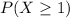 . Then
. Then
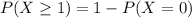
In which

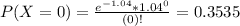
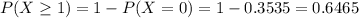
64.65% probability of at least one injury commuting to work in the next 20 years