Question

The triangle T has vertices at (-2, 1), (2, 1) and (0,-1). (It might be an idea to

sketch it.) Write down a double integral equal to its area and evaluate it.
(3 marks)​

Answer 1

Rewrite the boundary lines y = -1 - x and y = x - 1 as functions of y :

y = -1 - x ==> x = -1 - y

y = x - 1 ==> x = 1 + y

So if we let x range between these two lines, we need to let y vary between the point where these lines intersect, and the line y = 1.

This means the area is given by the integral,

`\displaystyle\iint_T\mathrm dA=\int_(-1)^1\int_(-1-y)^(1+y)\mathrm dx\,\mathrm dy`

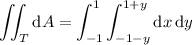
The integral with respect to x is trivial:

`\displaystyle\int_(-1)^1\int_(-1-y)^(1+y)\mathrm dx\,\mathrm dy=\int_(-1)^1x\bigg|_(-1-y)^(1+y)\,\mathrm dy=\int_(-1)^1(1+y)-(-1-y)\,\mathrm dy=2\int_(-1)^1(1+y)\,\mathrm dy`

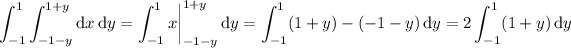
For the remaining integral, integrate term-by-term to get

`\displaystyle2\int_(-1)^1(1+y)\,\mathrm dy=2\left(y+\frac{y^2}2\right)\bigg|_(-1)^1=2\left(1+\frac12\right)-2\left(-1+\frac12\right)=\boxed{4}`

Alternatively, the triangle can be said to have a base of length 4 (the distance from (-2, 1) to (2, 1)) and a height of length 2 (the distance from the line y = 1 and (0, -1)), so its area is 1/2*4*2 = 4.