Answer:
The equation is represented 3 units to the left of the complex plane and 2 units up.
Step-by-step explanation:
Well to see how this is represented, we first need to multiply it out so we can see how it looks when it is simplified!
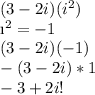
We know that on a complex plane, our imaginary numbers are represented on the vertical axis.
So the original expression, (3-2i) would have been 3 units to the right on a complex graph and 2 units downward!
The equation I input above should be pretty straightforward, but one thing I didn't mention was that i^2 should = -1 when dealing with complex numbers!
Therefore, the equation 3-2i * i^2 is equal to -3 + 2i, this is graphed 3 units to the left and to units upward!
If you notice, this is the exact opposite of the original equation! Why? Well it's because we simply multiplied by negative 1!