Answer:
D. 20 ft
Explanation:
Use pythagorus! We can imagine the rectangle is split into 2 equal triangles, one side of the triangle being 12, and the width being 16.
Pythagorus theorum is used to calculate the hypotenuse (long side) of a right-angled triangle. This is the formula:
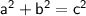
So, we do 12^2 (squared) + 16^2 =
144 + 256 = 400
Now, we have to find the square root of 400, which is equal to
20
So our answer is 20ft
Hope this makes sense! If you need further explanation, do let me know...
- profparis